挑战最快 SVM！ReHLine 算法诞生记

本文由邱怡轩主笔，内容素材源自邱怡轩和戴奔共同讨论的结果。

武林至尊，宝刀屠龙。长久以来，机器学习江湖中一直流传着两件神器——LibSVM 和 Liblinear，它们都是用来求解支持向量机（SVM）问题的，且都是由台湾大学的林智仁教授及其团队开发和维护。两者的不同在于，LibSVM 支持各类基于核函数的 SVM，而 Liblinear 只能计算线性 SVM。但从计算效率上来说，LibSVM 随样本量 $n$ 增加的复杂度大约在 $O(n^2)$ 到 $O(n^3)$ 之间，而 Liblinear 则几乎是线性的复杂度 $O(n)$。因此，如果考虑使用线性模型，那么 Liblinear 基本可以说是求解 SVM 的性能天花板。

用具体的公式来表达的话，线性 SVM 求解的是如下的最优化问题：

$$ \min_{\beta \in \mathbb{R}^d} \frac{C}{n} \sum_{i=1}^n ( 1 - y_i \beta^\intercal \mathbf{x}_i )_+ + \frac{1}{2} \Vert \beta \Vert_2^2,\qquad\qquad (1) $$

其中 $\mathbf{x}_ i \in \mathbb{R}^d$ 代表了第 $i$ 个观测的自变量向量, $y_i \in \{-1, 1\}$ 是一个二元的标签，$(x)_+=\max\{x,0\}$，而 $C$ 是一个表示分类代价的超参数。

为了更直观地展现 Liblinear 的影响力，我们可以打开谷歌学术搜索一篇发表在 Journal of Machine Learning Research 上的文章，LIBLINEAR: A library for large linear classification。截至文本写作的时间点，这篇论文已经被引用了9674次，恐怖如斯。而从 Liblinear 的官网也可以发现，在世界各地的研究者和开发者的贡献下，Liblinear 也有了各种语言的接口：R、Python、Matlab、Java、Perl、Ruby，甚至全世界最好的语言 PHP——Liblinear 的流行程度可见一斑。

那么 Liblinear 这柄屠龙宝刀是否就从无敌手，一直号令天下呢？属于 SVM 江湖的倚天剑又流落何方？我们的故事，便由此说起。

Talk is cheap. Show me the code.

Linus Torvalds 有一句名言：“Talk is cheap. Show me the code.” 既然是江湖规矩，我们便直接上擂台。Liblinear 的代码是公开的，同时为了避免脚本语言的执行效率造成性能损失，我们直接使用原生的 C++ 代码进行测试。使用的数据来自于 LibSVM Data 页面，它是由 LibSVM 的开发团队整理的数据集合。我们选取其中的一个名为 SUSY 的数据，它包含500万个观测和18个自变量，因变量是二分类，数据以文本形式存储大约是2.3 GB 大小。我们对 Liblinear 的代码进行了轻微的修改，使其可以记录计算所消耗的时间。

编译并运行 Liblinear 程序后，我们得到如下的输出结果：

......**
optimization finished, #iter = 64
Objective value = -58.018530
nSV = 3122272
Computation time: 9.574224 seconds.

由此可以看出，Liblinear 仅仅使用了9.57秒就完成了计算（不包含数据读取的时间）。

而接下来要登场的挑战者，是我们编写的一个名为 ReHLine-SVM 的软件。ReHLine-SVM 本身只包含一个 C++ 头文件 rehline.h，也就是说它可以直接嵌入到其他的 C++ 项目中，无需单独进行编译。ReHLine-SVM 的底层代数运算是由著名的科学计算库 Eigen 实现的。

我们用 ReHLine-SVM 来对同一个数据计算 SVM，并将各类超参数设成与 Liblinear 相同的取值。其最终的输出结果如下：

Iter 0, dual_objfn = -45.7268, primal_objfn = 66.7088, xi_diff = 0, beta_diff = 21.9285
*** Iter 21, free variables converge; next test on all variables
Computation time: 3.35343 seconds

这个结果表明，ReHLine-SVM 只用了3.35秒就完成了计算！但这还不是故事的全部：由于不同的算法其收敛条件和精度不尽相同，因此为了结果的公平，我们还要看一个更客观的指标——SVM 的目标函数值，也就是本文开篇写下的公式 (1)，其取值越小代表越接近最优解。经过计算，Liblinear 和 ReHLine-SVM 得到的目标函数值均为58.0185。由此我们终于可以说，ReHLine-SVM 仅仅使用了不到一半的时间，就取得了和 Liblinear 相同水平的解——我们似乎找到了 Liblinear 的一名合格的挑战者。

他山之石

时间倒回到两年半以前，有一次我和戴兄（本故事的主角）聊起统计计算，我们都对林智仁教授团队的工作赞不绝口。戴兄是 SVM 方面的专家，于是特别提到 Liblinear 强悍的性能，并分享了他对 Liblinear 算法的研究心得。他当时提到，SVM 与分位数回归具有一些内在的相似性，如果 Liblinear 能很好地解决 SVM，那么应该也能用来计算分位数回归。

有了这个初步的想法，我和戴兄便一拍即合，准备把 Liblinear 的算法好好研究一下，然后尝试将其拓展到其他的统计模型上。接下来故事的发展完全按照预想的剧本进行——毫不意外地，我的拖延症犯了，而且一拖就是一年多。好在戴兄终于把我拉了回来，我才开始认真学习起 Liblinear。

要弄明白 Liblinear 为什么如此强大，就要了解其背后所使用的算法。SVM 的目标函数 (1) 是一个不那么容易求解的问题，因为 $(x)_+$ 是不可导的，通常的梯度下降法并不适用。但是，我们可以考虑 (1) 的对偶问题，也就是说它等价于求解下面这个优化问题：

$$ \min_{\alpha \in \mathbb{R}^n} \frac{1}{2}\alpha^{\intercal}Q\alpha-\mathbf{1}^{\intercal}\alpha\quad\text{subject to}\quad 0\le\alpha_i\le C/n,\ i=1,\ldots,n,\qquad\qquad (2) $$

其中 $Q$ 是一个 $n\times n$ 的矩阵，且 $Q_{ij}=y_i y_j \mathbf{x}_i^{\intercal}\mathbf{x}_j$。这个新的问题优化的是另一个向量 $\alpha$，但它与原问题的变量 $\beta$ 之间具有紧密的联系：

$$ \beta=\sum_{i=1}^n \alpha_i y_i \mathbf{x}_i.\qquad (3) $$

换言之，只要我们能获得 (2) 的最优解 $\alpha^*$，我们就可以利用 (3) 来得到 $\beta$ 的最优解 $\beta^*$。那么为什么 Liblinear 要转而解决问题 (2) 呢？其中一个很重要的原因在于，(2) 是一个带箱型约束的二次规划问题，可以很容易地通过坐标下降算法（coordinate descent，CD）求解。直观来说，CD 就是每次只优化 $\alpha$ 的一个分量，等每个分量都遍历一遍后再从头开始，直到总体的目标函数值收敛。每次只优化一个分量的好处是，单个分量的最优解往往具有显式的表达式，例如对于 (2) 来说，在固定其他分量的取值时，$\alpha_i$ 的最优解可以写为

$$ \alpha_i^{\mathrm{new}}\leftarrow\alpha_i+\delta_i,\quad \delta_i=\max\left(-\alpha_i,\min\left(C/n-\alpha_i,\frac{1-(Q\alpha)_i}{Q_{ii}}\right)\right),\qquad (4) $$

其中 $(Q\alpha)_i=y_i\mathbf{x}_i^{\intercal}(\sum_{j=1}^n \alpha_j y_j \mathbf{x}_j)$。不难看出，更新一次 $\alpha_i$ 其计算量主要在 $(Q\alpha)_i$ 之上，量级为 $O(nd)$。而要把 $\alpha$ 的所有分量更新一次（我们通常称此为一次算法迭代），则显然需要 $O(n^2 d)$ 的计算量，这在样本量 $n$ 很大时是个不小的成本。

但 Liblinear 的精髓之处就在于用 (3) 式去替换 $(Q\alpha)_i$ 的表达式，即 $(Q\alpha)_i=y_i\mathbf{x}_i^{\intercal}\beta$。换言之，如果我们知道了 $\beta$ 的取值，那么 $(Q\alpha)_i$ 就只需要 $O(d)$ 的计算量，这将是本质的差别！当然，因为 $\alpha$ 和 $\beta$ 是彼此关联的，所以每次更新完一个 $\alpha_i$ 后，$\beta$ 也需要进行相应的更新，对应的算法如下：

$$ \delta_i=\max\left(-\alpha_i,\min\left(C/n-\alpha_i,\frac{1-y_i\mathbf{x}_i^{\intercal}\beta}{Q_{ii}}\right)\right),\quad \alpha_i^{\mathrm{new}}\leftarrow\alpha_i+\delta_i,\quad \beta^{\mathrm{new}}\leftarrow\beta+\delta_i y_i \mathbf{x}_i.\quad (5) $$

如此同时更新 $\alpha$ 和 $\beta$，一次算法迭代便只需要 $O(nd)$ 的计算量，比之前的 $O(n^2 d)$ 整整少了一个 $n$ 的倍数。而 Liblinear 算法的另一个重要性质是，这样的迭代至少是线性收敛的，也就是说优化的误差会随着迭代次数的增加而呈现指数级的下降。最后再加上林教授团队优秀的软件和工程能力，各项因素综合在一起便成就了 Liblinear 屠龙宝刀的江湖地位。

石中藏玉

在搞明白了 Liblinear 的原理之后，我们便开始重新思考戴兄之前的想法，即如何把“CD 算法+线性复杂度”这套方法应用到其他的统计问题之上，例如分位数回归。我们注意到 SVM 的损失函数本质上就是一个 ReLU 函数，$\mathrm{ReLU}(x)=\max(x,0)$，于是便设想，如果某个损失函数能表达成 ReLU 函数的求和，那应该就可以复制 Liblinear 的成功。

事实证明戴兄的这个直觉是非常准的，而且更加幸运的是，我们发现 Liblinear 所使用的算法还可以得到极大的扩展，从而用来解决更大的一类问题。最终，我们关注的是如下的一类最优化问题：

$$ \min_{\beta \in \mathbb{R}^d} \sum_{i=1}^n L_i(\mathbf{x}_i^\intercal \beta) + \frac{1}{2} \Vert \beta \Vert_2^2 \quad\text{subject to}\quad A\beta+b\ge 0,\qquad (6) $$

其中 $L_i(\cdot)$ 代表第 $i$ 个观测上的损失函数，而 $A\beta+b\ge 0$ 是一个一般的线性约束。事实上，很大一类的统计和机器学习模型都可以表达成这种“损失+正则项+约束”的形式，而不同模型的区别往往主要体现在损失函数 $L_i(\cdot)$ 之上。我们后来发现，当 $L_i(\cdot)$ 具有如下的形式时，我们便可以构造出高效的具有线性复杂度的 CD 算法：

$$ L(z)=\sum_{l=1}^L \mathrm{ReLU}(u_l z+v_l)+\sum_{h=1}^H \mathrm{ReHU}_{\tau_h}(s_h z + t_h),\qquad (7) $$

其中

$$ \mathrm{ReHU}_\tau(z) = \begin{cases} \ 0, & z \leq 0 \\ \ z^2/2, & 0 < z \leq \tau \\ \ \tau( z - \tau/2 ), & z > \tau \end{cases}. $$

更有意思的是，戴兄还证明了，(7) 式中的 $L(z)$ 实际上等价于凸的分段线性-二次函数。换言之，只要 (6) 中的损失函数是凸函数且能被分段的线性或二次函数逼近，那么就可以使用我们设计的算法高效地求解——这是一类远比 SVM 更一般和广泛的问题。下图展示了一些常见的损失函数的图像，它们都包含在这个范围之内。

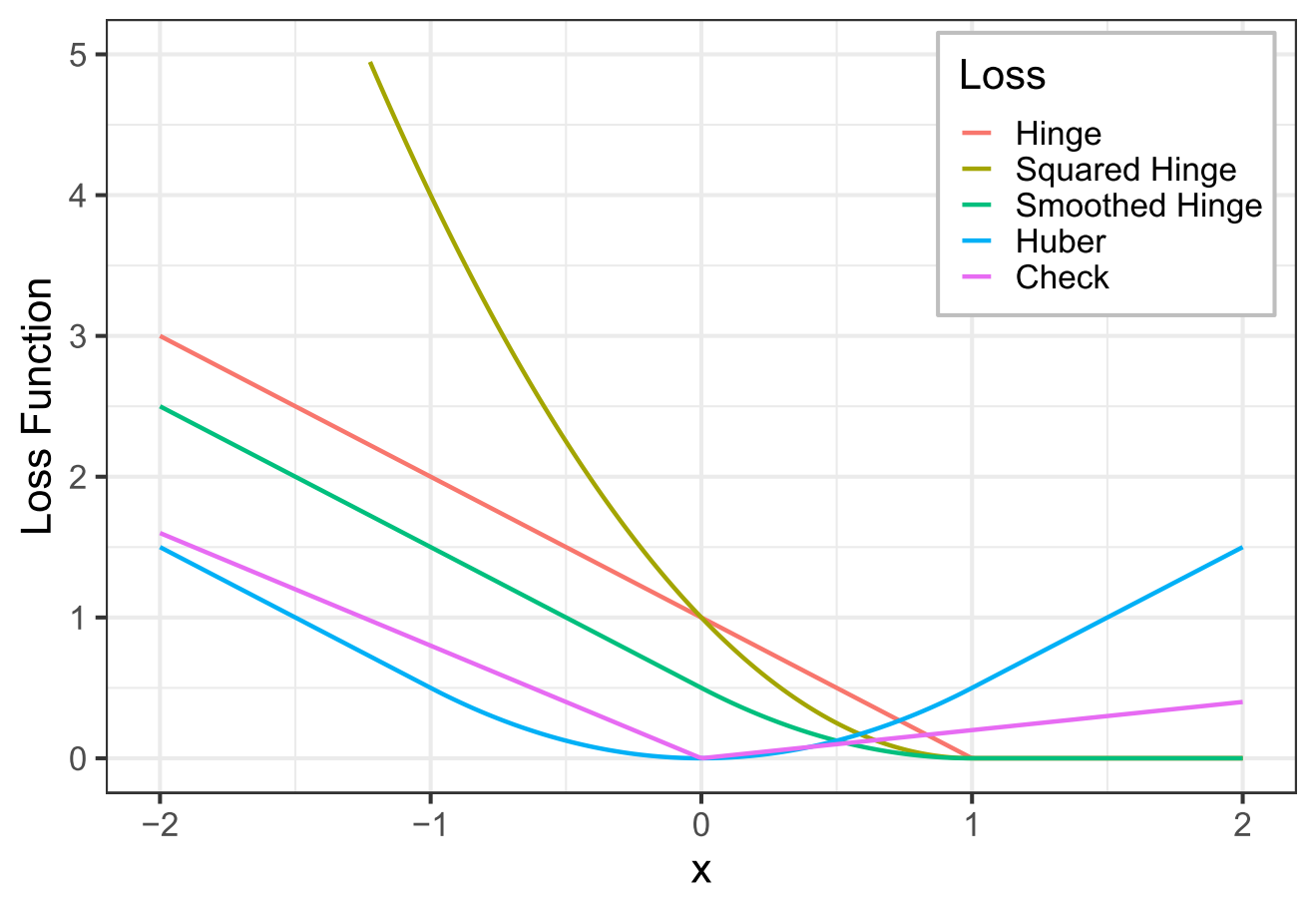
事实上，虽然戴兄最初只是想设计一个算法来解决分位数回归的计算，但最终我们得到了更多：分位数回归，Huber 回归，平滑 SVM，带公平性约束的 SVM，等等。

挑战者

我们最终将这个新提出的算法命名为 ReHLine，它的前半部分来自于 (7) 式中的 ReLU-ReHU 分解，而后半部分的“Line”则是体现了 ReHLine 的四条“线性”性质：

• 适用于任意的凸分段线性-二次损失函数
• 可加入一般的线性约束
• 优化算法具有线性的收敛速度
• 一次算法迭代的计算复杂度线性于样本量

戴兄还发现，Reh 也是一种鹿的名字（其实更接近我们的东北神兽（傻）狍子），鹿和狍子跑得快，也是一个好的意象。于是我用 AI 工具画了一张 ReHLine 的 logo，就是一只正在下坡奔跑的傻狍子，寓意快速地奔向目标（函数）的最低点。

在我们设计出 ReHLine 算法后，便希望对它做一些测试，而一个很自然的想法就是看看它与 Liblinear 之间的对比。我们怀着无比忐忑的心情用 ReHLine 跑了一下 SVM，之所以忐忑，是因为我们都清楚 Liblinear 的强大。因此，我们其实只期待 ReHLine 不要落后 Liblinear 太多就心满意足了，因为 ReHLine 的主要优势在于可以解决 SVM 之外的问题，而 Liblinear 经过了这么多年的开发，又是专门针对 SVM 优化的，所以应该是很难超越的。

然而结果大大超出了我们的预料。如上面 ReHLine-SVM 的实验，实际跑出来的结果，ReHLine 计算 SVM 居然比 Liblinear 还要快！我们一开始根本不敢相信这个结果，因为从情感上说，我们都对林教授的工作有很强的认同感和崇拜感，觉得战胜武林至尊是一件不可思议的事；另外从理性上来说，我们知道 ReHLine 是受 Liblinear 启发而来，而且它在 SVM 问题上就等价于 Liblinear 的算法。最后经过反复的验证，我们还是接受了这个事实。我们的猜测是虽然 ReHLine-SVM 在算法上是等价于 Liblinear 的，但或许一些底层的工程实现让 ReHLine-SVM 取得了更高的计算效率。而在其他的模型中，ReHLine 不管是对上专用的算法还是通用的求解器，都取得了喜人的结果。具体的对比结果可以在我们的 ReHLine 基准测试中查看。

尾声

在完成了 ReHLine 的项目之后，我和戴兄便商量是不是该宣传宣传这个工作，以及应该以一个什么切入点来介绍。后来我一拍脑袋，说要不就蹭一蹭 Liblinear 的江湖地位吧，用一个唬人的标题，把人骗进来再说。于是为了这个震惊体标题，我们就单独编写了文中提及的 ReHline-SVM 软件，直接对标 Liblinear。（顺便求一个 Star-Follow-Fork 三连！）

事实上在编写 ReHLine-SVM 之前，我们已经有了更通用的 ReHLine 算法求解器。相关的论文、代码和文档都可以在项目主页中找到，同时我们还提供了 Python 和 R 的接口。如果你喜欢我们的这个工作，还请不吝在 Github 上给我们加加星，表达一下对我们的支持。

笔墨至此，或许终究还是有自卖自夸之嫌，但无论如何，ReHLine 对我们来说都是一次非常独特的探索之旅。我们希望尽可能还原这条探索之路上的想法和感悟，若是它们能为更多的同行者提供些许灵感和激励，便也不枉此行了。

作者简介：邱怡轩，上海财经大学统计与管理学院副教授，统计之都理事会成员，研究方向包括深度学习、生成模型和大规模统计计算等，是众多开源软件的作者和维护者，个人主页 https://statr.me/。戴奔，香港中文大学统计系助理教授，主要研究领域包括机器学习、学习理论、因果推断和统计计算等，开发了众多统计与机器学习软件，个人主页 https://bendai.org/。